Красоту деревьев для восприятия объяснили математически

Художественная красота может быть вопросом вкуса, но наша способность распознавать деревья в произведениях искусства связана с объективной — и довольно простой — математикой. Таковы выводы авторов нового исследования в журнале PNAS Nexus.
Ученые выявили одну величину, связанную со сложностью и пропорциями ветвей дерева, которую художники используют, чтобы повлиять на восприятие деревьев на своих полотнах.
«Мы пришли к чему-то универсальному, что применимо ко всем деревьям в искусстве и природе. Это лежит в основе многих различных изображений деревьев, даже если они выполнены в разных стилях, культурах или веках», — отметил доцент кафедры сложных систем Мичиганского университета Митчелл Ньюберри.
Фракталы
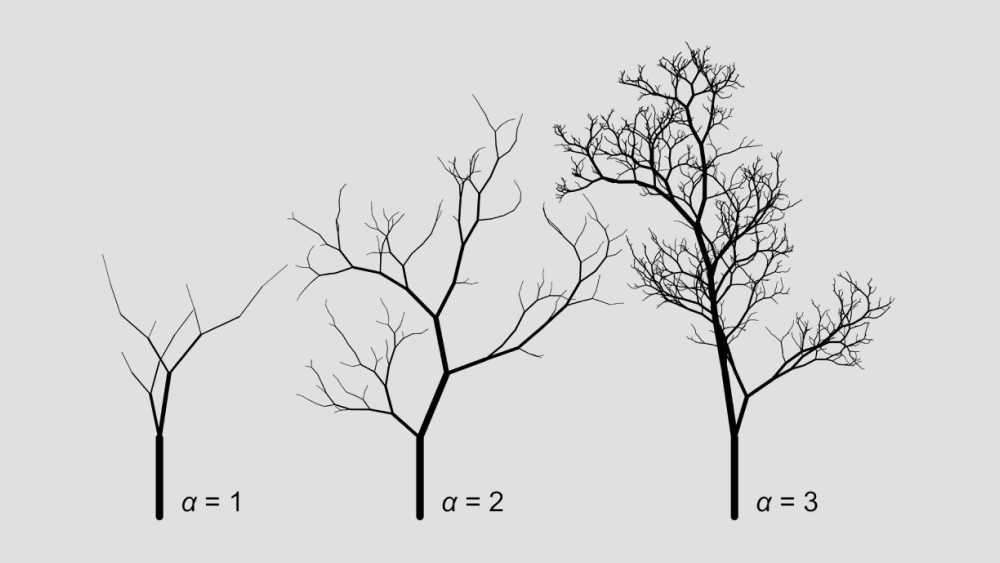
Математически деревья можно описать фракталами — самоповторяющимися ветвящимися структурами.
«Фракталы — это просто фигуры, которые повторяют сами себя. Если вы посмотрите на дерево, его ветви ветвятся. Затем дочерние ветви повторяют фигуру родительской ветви», — рассказала Цзинъи Гао, которая в пору написания статьи была студенткой бакалавриата Мичиганского университета.
Во второй половине XX века математики ввели число для количественной оценки сложности фрактала — фрактальную размерность. Аналогичный показатель есть в исследовании Гао и Ньюберри — они назвали его экспонентой масштабирования диаметра ветвей.
«Мы измеряем масштабирование диаметра ветвей на деревьях, и она играет ту же роль, что и фрактальная размерность. Она показывает, сколько еще мелких ветвей появляется при увеличении масштаба», — пояснил Ньюберри.
Авторы работы постарались сделать ее максимально доступной даже для тех, кто далек от искусства и точных наук. Математическая сложность уравнений ограничивается знаменитой (или печально известной, в зависимости от вашей успеваемости по геометрии в школе) теоремой Пифагора: a2+b2=c2.
Грубо говоря, a и b можно рассматривать как диаметр меньших ветвей, отходящих от более крупной ветви с диаметром c. Степень 2 соответствует экспоненте масштабирования диаметра ветвей, для реальных деревьев ее значение должно входить в диапазон от 1,5 до 3.
Этот параметр оказался ключевым — как бы ни было нарисовано дерево, при соблюдении экспоненты оно легко распознается даже в отличие любых других художественных признаков.
Художественные эксперименты
Ученые проанализировали множество различных произведений искусства — от каменных резных окон мечети Сиди Сайид в Индии (которые их, вообще говоря, и вдохновили) до «Вишневого цвета» японского художника Мацумуры Госюна.

Но самым богатым материалом для исследования стали картины голландского художника Пита Мондриана. В начале XX века он написал серию полотен, изображающих одно и то же дерево — но в разных, все более абстрактных стилях.
Ньюберри предложил сравнить две работы живописца.

«Серое дерево» 1911 года состоит из черных штрихов на сером фоне.
«Если вы покажете эту картину кому-либо, это очевидно дерево, хотя там нет цвета, нет листьев и даже ветвления, на самом деле», — заверил ученый.
Экспонента масштабирования ветвей Мондриана входит в диапазон реальных деревьев — 2,8. Однако для его работы 1912 года «Цветущая яблоня» это масштабирование отсутствует, как и понимание, что это нарисованный объект похож на дерево.
«Люди видят танцоров, рыбью чешую, воду, лодки — все что угодно. Единственное различие между этими двумя картинами — они обе представляют собой черные штрихи на практически сером фоне — это наличие масштабирования диаметра ветвей», — подытожил Митчелл Ньюберри.